科研随想 (21.09)
Multivariate Time Series
多变量时序(MTS)这个 Topic,主要是两个方面,预测和异常检测(后者事实上也可以通过预测来得到结果)。
目前根据咱的方向,主要是做基于图的时序数据挖掘,事实上在大多数论文中,这被分成了两个步骤:
- 首先通过时序数据,提取特征,构建图模型。
- 然后使用基于图的机器学习模型,完成给定的任务。
组会相关
这次组会主要有提及三种不同的在时序数据上构建图的新方法。
MTAD-GAT
这篇文章总的来说,就是在上述两个阶段上分别结合了两个不同特点的模型。
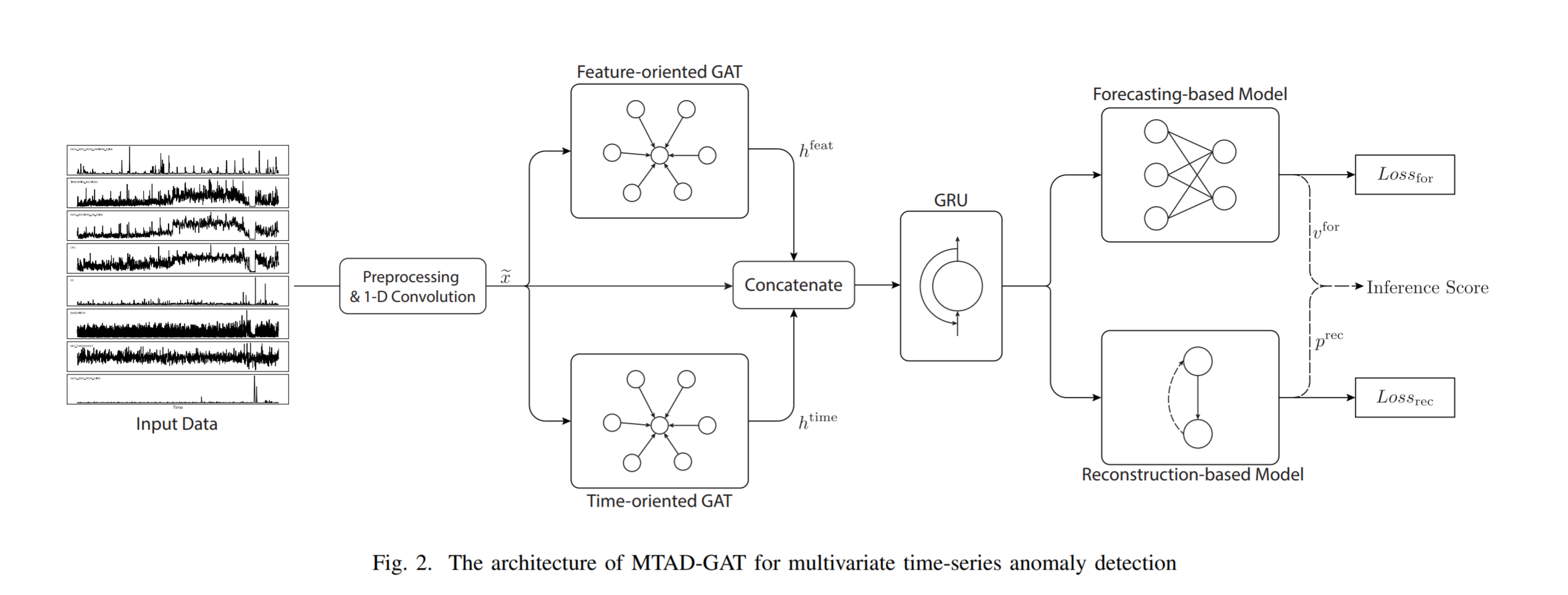
图的构建:预处理和两套 GAT
预处理里这个 1-D 卷积是在时间方向进行的,从信号的角度讲,是提取每条序列中与时间无关的特征。
后面的两个 GAT 算是多元时序数据上的老套路新利用,从横(时间)纵(特征)两个维度出发来生成图,分别捕捉时间与空间上的特征,它们分别是:
- 基于特征(Feature-Oriented)的 GAT:将每一条序列作为节点,边反映它们间的关系。
- 基于时间(Time-Oriented)的 GAT:将每一个滑动的时间窗口作为节点,边反映这些窗口下数据之间的关系。
学习模型:基于重构和基于预测
基于预测的模型,是用于预测下一时间的结果(正向),而基于重构的模型,是用于从图的表征中学习时间序列数据的分布(反向),最后的 Loss 则是它们相加的结果。
评价
这篇看上去中规中矩,思路是从不同的逻辑方向组合模型,不过有些怀疑结果会依赖数据处理时候的 Sliding Window 的选取。
GDN
抱歉摸鱼去了没看懂,大概也是个端到端的基于图的异常检测。
EvoNet
这个文章让人立即想到了 Time Series Chain 以及一大堆看着很像 FSM 的东西。
它的 Moltivation 来源于,认为时间序列数据在不同的状态之间改变,正如在一个图中的若干节点间游走,而同时这个图本身在随时间变化,此之谓 Evolution。
State Graph
这个 State,或者也可以称为 Motif,指的是一小段时间内的时间序列片段,它可能会一次或多次地在时间序列数据中出现。
何为 State Graph?它被定义为了对外表征为一个 Segment ($X_t$) 的组成元素的不同权重组合和变化趋势。
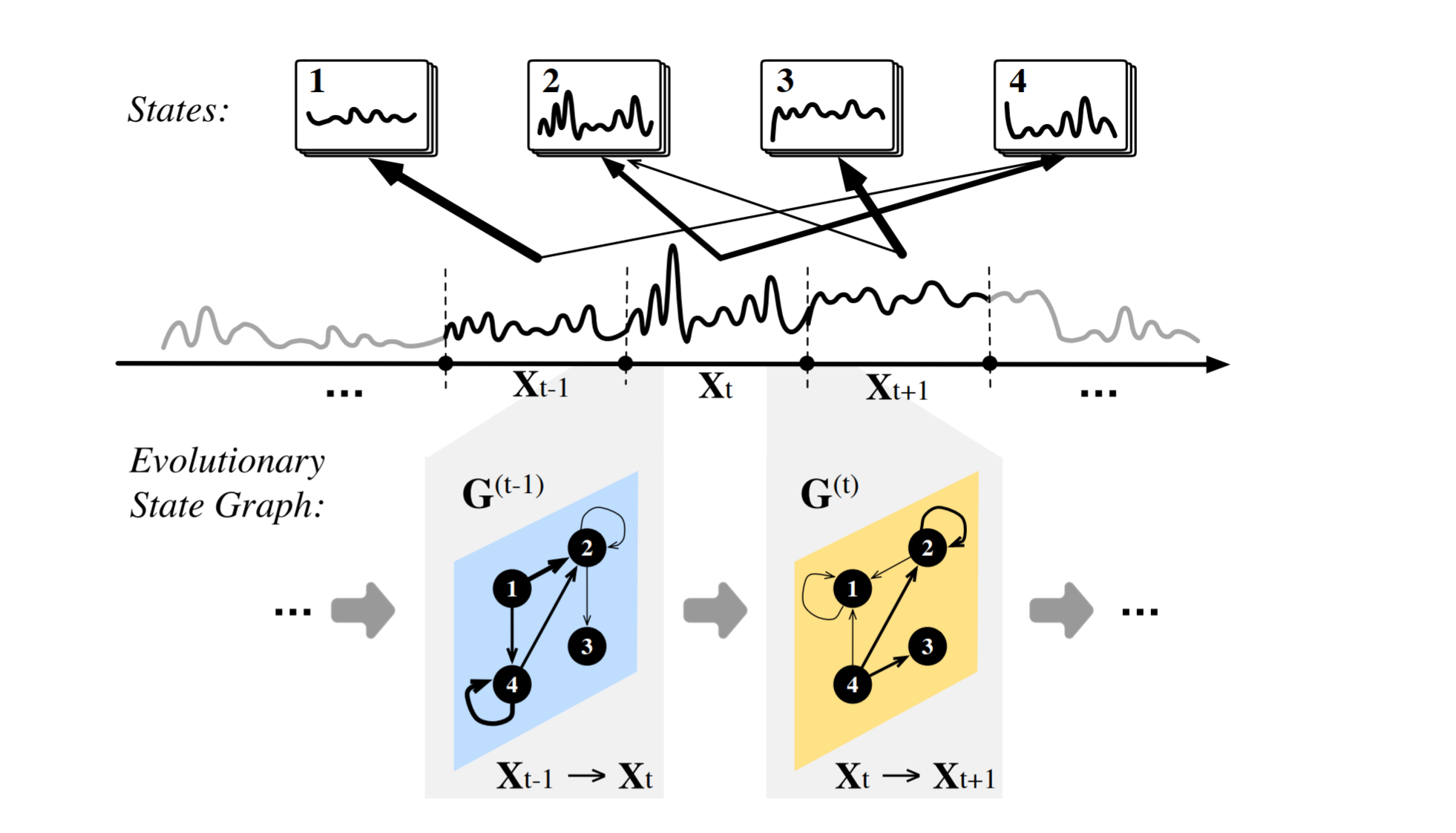
从图中可以看出来,以 State ($\Theta_v$) 作为多个 Node 组成的 Graph ($G^{(1:T)}=\langle V, E, M \rangle$),在某种意义上,事实上指的就是时间序列数据中,不同模式所构成的状态机/马尔科夫链 ($X_{t-1} \to X_t$)。
Evolution
如果说到此为止的话,可能跟那篇 TSC 的论文以及后续提出的从多个角度诠释 TSC 的论文基本一致了,甚至配图都基本差不多,所以作者在后面又提出了新的东西:要认为这是一个变化的 State Graph,它们的权重在不同的时间是不一致的,这最终与上一个时间窗口的 Segment ($X_{t-1}$) 结合计算出当前时间窗口的 Segment ($X_t$),实质上是 Transition Weight ($m^t_{(v,v’)}$)。
$$ m^t_{(v,v’)} = P(\Theta_{(v,v’)}|X_{(t-1,t)}) = P(\Theta_v|X_{t-1}) \times P(\Theta_{v’}|X_t) $$

这就与静态的图模型大不相同了,它不仅能从 State Graph 中去获取 Local 的信息,并生成结构化的图模型,还能通过 Transition of States 来对时间上的变化进行建模。
评价
个人认为是某种程度上 TSC 的改进,使用动态图对演进的时间特征进行建模,使得其相对于静态的构建关系图的方法在时间维度和可解释性上更具优势。(作者也是这样吹的)。总的来说,方向都是将时间序列片段(或 特征/Motif)作为 Node,将其转化为节点间游走的概率权重问题,然后通过模型去学习这样的权重。
不过这里依然存在第一篇论文所说的,需要专家知识以确定 Segment 或设定窗口长度超参数($\tau$)等。
总结
以上论文涉及了两种思路,一个是将时序数据从横纵两个维度切开,分别去进行图的构建,另一个是先提取特征片段及其之间的关系,然后再使用图来对整个时间序列的演化进行建模。
从第一篇中可以获得一个,将时间/空间结合成一个异质图网络的结构的想法。
而第二篇则反映出了时间序列数据潜在的规律性可以被精确建模为“类状态机”的形式,联想到利用随机游走可以获得一些信息,同时这种依赖人工确定窗口长度的模型是否能有改进的空间也值得思考。